SOMMAIRE

*** FC comme valeur d'extrapolation des capacités maximales ***
FC comme indice de l'intensité de l'exercice
FC comme indice de récupération

FC comme valeur d'extrapolation des capacités maximales

Problèmes inhérents à l'utilisation de la fréquence cardiaque maximale (FCM)

Compte tenu de toutes les fluctuations auxquelles est sujette la FC, il est bon de s'interroger sur la validité et l'interprétation de la mesure de la fréquence cardiaque maximale (FCM) ou sous-maximale dans une évaluation des capacités maximales d'un individu effet, depuis que Wyndam (1959) a confirmé la relation linéaire entre la FC et la consommation d'oxygène (VO₂), beaucoup se sont penchés sur l'évaluation indirecte de VO₂ pour estimer les capacités maximales d'un sportif (Astrand et coll., 1964 ; Astrand et Rhyming, 1954 ; Astrand et Saltin, 1961 ; Conconi et coll., 1982 ; Davies et coll., 1972 ; Fox, 1973).
Or, il s'est avéré que les extrapolations à partir de FCM pouvaient être entachées d'erreur. Certains auteurs (Cazorla et coll., 1984 ; Davies, 1968 ; Leymonie, 1984 ; Viladin et coll., 1989) ont montré que des sous- et surestimations apparaissent facilement dès lors que l'on utilise une valeur de FC calculée à partir d'une valeur (ou série de valeur) sous-maximale, ou que l'on utilise la FCM théorique (voir plus loin).
Plusieurs raisons peuvent être invoquées pour justifier cette constatation :

• pour un même individu, FCM varie de ± 5 battements par minute ;
• pour un même groupe d'âge, cette fluctuation est d'environ 10 %;
• les tests sous-maximaux sont de très mauvais outils d'extrapolation dès lors qu'ils sont appliqués au sportif chez qui les fluctuations de FC n'ont rien de commun avec celles des sédentaires.

Il en va de même pour la méthode de détermination du "seuil aérobie-anaérobie" proposée par Conconi et coll. (1982) sévèrement critiquée et remise en cause par certaines études publiées ultérieurement (Lacour et coll., 1987 ; Léger et Tokmakidis, 1987).
Pour palier à ces erreurs, il est préférable, comme nous l'avons dit plus haut, de mesurer la FCM individuellement grâce à un exercice exhaustif, et, ensuite, d'utiliser des valeurs relatives (pourcentage) dans l'élaboration des suivis d'entraînement. Certains (Astrand et Rodhal 1980 ; Taylor et coll., 1969) ont proposé de mettre en relation le pourcentage de VO₂max avec celui de la fréquence cardiaque ou, mieux, de la réserve cardiaque fonctionnelle maximale (voir plus loin). L'erreur d'estimation avec cette seconde méthode n'est plus que de ± 8%. Cette relation est influencée par l'âge des sujets. Par exemple, les enfants de 6 ans auront, pour un même pourcentage de V0₂ max, des valeurs de FCM plus élevées en pourcentage que de jeunes adultes de 18 ans, comme l'illustre la figure 1 ci-dessous. Cette différence s'atténue avec l'âge.

Figure 1 : Relation entre %VO₂ et %FC pour deux classes d'âge

La réalité sur la formule estimant la fréquence cardiaque maximale théorique (FCMT)

Le problème majeur pour utiliser la FC, comme outil d'estimation de l'intensité de l'exercice, est l'évaluation de la FCM.
Beaucoup d’ouvrages de physiologie prônent l’utilisation de la formule : FCMT = 220 – âge, pour estimer la fréquence cardiaque maximale théorique (FCMT) d’une personne en vu de gérer l’intensité de l’exercice. Or, depuis de nombreuses années, nous savons que cette relation n’est pas fiable.
Cette formule n’est en fait qu’une approximation obtenue par Haskell et Fox (1970) en traçant une droite passant au plus près de la majorité des valeurs de FCM (meilleur ajustement linéaire de façon manuelle) reportées sur un graphe construit à partir d'une compilation d'articles scientifiques (Figure 2 ci-dessous). En refaisant un vrai calcul de la droite de régression passant par les valeurs de fréquence cardiaque maximale (FCM) de 35 des 42 expériences (du fait d’erreurs dans la bibliographie de l’article) regroupées sur cette figure, Robergs et Landwehr (2002) ont trouvé la relation suivante :

Figure 2 : Reproduction de la figure de Fox et coll. (1971) à l'origine de la formule 220-âge
(trait discontinu tracé sans calcul par les auteurs). Le trait bleu correspond à l'équation de la droite de régression donnée
en encart et calculée par Robergs et Lanwehr (2002) à partir des valeurs citées par Fox et coll.

Cette équation n’est évidemment pas similaire à celle initialement proposée de la FCMT. Et cela, nous le savons depuis 1938, avec la publication, par Robinson de la première équation de prédiction de FCMT (212 – 0,77 * âge).
Pour que la formule "220 – âge" soit acceptable, il faudrait que la pente de la relation entre la diminution de FC et l’augmentation de l’âge soit de 1… (c'est-à-dire avec une relation de la forme : "220 - âge x 1"). Ce n’est évidemment pas le cas au regard des valeurs publiées par Astrand et coll. (1952, 1973, 1997) regroupées ci-dessous dans la figure 3. On voit clairement que la relation entre FC et âge est curviligne et non linéaire ; la formule de FCMT n’est donc pas applicable aux sujets de moins de 10 ans.

Figure 3 : Reproduction de la figure de Astrand (1952) de FCM obtenues chez 225 sujets de 4 à 33 ans.

Et même si l’on fait abstraction de ce sous-groupe d'âge en ne gardant que les personnes d’un âge supérieur ou égal à 10 ans, on obtient la figure ci-dessous (figure 3) et l’on obtient l’équation indiquée au-dessus du graphe :

Figure 4 : Reproduction de la figure 3 mais en ne gardant que les sujets âgés entre 11 et 33 ans

Encore une fois, elle ne correspond pas à la formule de la FCMT de Fox et coll.
Robergs et Lanwehr (2002) ont fait une méta-analyse de 43 publications relatives à la FCM en ne retenant que les 30 études les plus complètes d'un point de vue statistique. Ils ont ensuite compilé les équations de régression pour calculer la FCM d'individus âgés entre 20 et 100 ans. Leur nouvelle équation de régression donne une formule prédictive suivante : FCM = 208,754 - 0,734 * âge (r = 0,93 ; erreur = ± 7,2).

Les méta-analyses qui ont été publiées à ce jour sur la FCMT (par exemple : Tanaka et coll., 2001 ; 208 - 0,7 * âge ; r = 0,81) donnent des formules très proches de celle-ci (Figure 5).

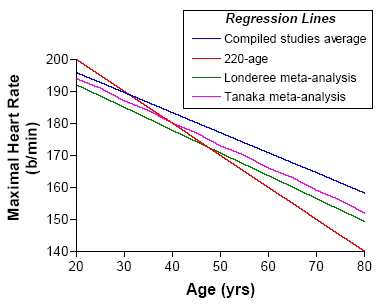
Figure 5 : Droites de régression obtenus à partir des méta-analyses publiées à ce jour sur la FMT (Robergs et Lanwehr, 2002).

Evaluation directe de FCM

Cette première méthode est de loin la meilleure. Elle s’obtient au cours d’un test triangulaire (progressif et maximal) ou lors d'un test rectangulaire. Dans les deux cas, il faut faire un échauffement approprié. L'obtention de cette valeur de FC est largement facilitée par l’utilisation d’un cardiofréquencemètre. L’avantage de cette méthode est que la FCM est immédiatement disponible et peut être mise en relation avec un autre paramètre, de terrain (VMA) ou de laboratoire (VO₂max) par exemple, pour affiner l’optimisation des séances d’entraînement. Qui plus est, elle est strictement individuelle et participe donc à une meilleure gestion du potentiel de la personne.

NB : On ne peut s'appuyer sur les données issues d'un test d'effort réalisé par un cardiologue car ce n'est pas un test maximal par définition. Le médecin qui suit le protocole au sens strict du terme devra s'arrêter à 85% de la FCmax théorique estimée à partir... de la relation 220-âge (!). Le consensus dans la généralisation d'une autre formule valide et plus précise n'a toujours pas été réalisé comme standard par la communauté scientifique malgré les preuves qui s'accumulent contre son usage.

Evaluation indirecte de FCM

Elle ne peut être obtenue qu’à l’aide d’équations prédictives. Il faut définitivement abandonner la formule classique (220 – âge) pour les raisons évoquées plus haut. Mais, on sait aussi qu'à l’heure actuelle, aucune formule publiée n’est suffisamment précise pour être considérée comme fiable en toute circonstance ; les erreurs possibles de prédiction étant toujours trop importantes pour correspondre exactement aux intensités relatives de VO₂max souhaitées.
L’idéal serait que cette marge d’erreur soit réduite à 3 bpm (± 1,5 bpm) pour être acceptable.
Certains auteurs (comme Londeree et Moeschberger, 1982) ont même proposé des équations intégrant plusieurs paramètres : âge, âge², âge^4/1000, ethnie, mode d’exercice, niveau d’activité, type de protocole utilisé pour évaluer FC. Mais cela n'apporte rien de plus à la qualité de la prédiction et de sa précision.
Une autre approche serait de moduler le résultat en fonction des circonstances. Cette démarche a été adoptée par Miller et coll. (1993) qui propose une formule intégrant les résultats de travaux publiés récemment relatifs aux particularités de publics testés comme la variation de FCM en fonction du mode de test utilisé (course, vélo, nage ; Kravitz et coll., 1997 ; Tanaka et coll., 1991 ; Cassady et Nielsen, 1992) ou sa diminution avec l'entraînement d'endurance (Zavorsky, 2000). Ainsi, on peut calculer FCM à partir de l'équation de Miller et coll. : 217 - 0,85 * âge. Puis, on ajuste le résultat à partir des données suivantes :
•  utiliser cette formule pour l'entraînement de course et d'escalade ;
•  soustraire 3 bpm pour l'entraînement d'aviron ;
•  soustraire 5 bpm pour l'entraînement de cyclisme ;
•  soustraire 3 bpm pour les athlètes d'élite de moins de 30 ans ;
•  ajouter 2 bpm pour les athlètes d'élite de plus de 50 ans ;
•  ajouter 4 bpm pour les athlètes d'élite de plus de 55 ans.
La formule qui possède l’une des marges d’erreur les plus petites est celle de Inbar (205,8 – 0,685 * âge ± 6,4 ; formule obtenue au cours d’une étude réalisée avec 1424 sujets des deux sexes, âgés entre 20 et 70 ans pour une moyenne située à 46,7 ans ; Inbar, 1994).

Récemment, un bon qualitatif a été franchi, grâce à la publication des travaux de Gellish et coll. (2007) qui constituent une réelle avancée dans la validité de la FCmax de façon indirecte (Jackson, 2007).
Ils ont fait plus qu'une revue de la littérature puisqu'il s'agit d'un suivi longitudinal (c'est-à-dire les mêmes sujets suivis et testés pendant plusieurs années) entre 1978 et 2003 dans l'institut médical de l'université d’Okland (Michigan). Sur les 4666 personnes qui sont venues durant cette période et qui ont fait plus de 7000 tests maximaux (test de Balke sur tapis), seuls 100 hommes et 32 femmes ont été retenus pour avoir fait plus de 6 tests maximaux. Cet échantillon représente au total 908 tests administrés sur 25 ans. Et 90% sont de types caucasiens. Après filtrage des données, 697 tests ont été retenus chez les hommes et 211 chez les femmes. Ils ont été réalisés sur une période de 9±3,7 ans après l'élimination du premier test dit d'accoutumance. C'est la première étude du genre ! C'est aussi la plus fiable à l'heure actuelle comme en témoigne d'autres études publiées ultérieurement pour en tester la validité (e.g. Cleary et al. 2009).
Sa validité est restreinte à une population entre 30 et 75 ans pour une erreur type de ±5 à 8 battements dans sa forme linéaire, ce qui est quasi similaire celle de Inbar (tranche d’âge : 20-70 ans ; erreur-type : ± 6,4 bpm). Cependant, l’erreur tombe à ± 2 à 5 bpm entre 35 et 65 ans dans sa forme curvilinéaire. Ce qui en fait, à ce jour, la plus précise des équations pour estimer la FCMT.
Concernant la formule,  Gellish et coll. proposent :
- soit : 206.9 – (0.67 x âge) pour la relation linéaire ;
- soit : 191,5 – 0.007 x âge² pour la relation curvilénaire ;
Cette seconde formule est la plus valide des deux car elle épouse mieux la tendance de l’évolution globale de la FCM avec l’âge. Mais d'un point de vue pratique, certaines personnes préfèreront la formule linéaire pour sa simplicité d'utilisation, même si un tableau ou une calculatrice permet d’utiliser la seconde tout aussi facilement (sous la forme : 191,5 – âge x âge x 0,007).